On Self-Care and Science
If you are a scientist, like me, you probably like facts. We check COVID-19 numbers multiple times per day. We explain log-scale trajectories to our relatives. We read up on the details of serological assays.
And sometimes we lose track of priorities, we forget to take care of ourselves.
Most of us have long lists of self-care routines. Active things, like running and yoga. Mindful practices, like meditation and gratitude journaling. Seemingly basic habits, like hugging our kids or calling a friend. Silly things, like dancing it out around the kitchen isle.
In this post I will give a little background on some lesser known self-care practices that keep me afloat. I will even provide the scientific facts behind them, promised.
Here’s the list:
- Stairstep Breathing
- Self-Compassion
- Cold Showers
- Completing The Stress Cycle
- Turning Around Thoughts
- The Power Of Now
- Professional Help
I have been practicing all of these techniques over the last few years, some of them daily. I learned them from professionals – most notably from my therapist and from my yoga teachers.
As usual, the source of this post is available openly, please correct any mistakes.
Stairstep Breathing
If you have never done a breathing exercise before, this is the one to get started. Maybe it’s even the only one you will ever need, it is that good. I learned it from my sister-in-law, who is a clinical psychologist.
Start in a relaxed position. There’s no need for a cross-legged yoga posture, just use a chair. Or lay down on your back, the exercise is also very helpful to wind down at night.
For a couple of cycles, observe your breath without influencing it in any way. After your next exhalation:
- Fill your lungs by inhaling through your nose in a step-wise fashion
- Once your lungs are really full – pause…
- Breathe out through your nose in one very long and steady stream
- Mindfully observe how your body feels
- Rinse & repeat!
It may be helpful to use the metaphor of climbing a mountain:
- Climb up in about 5-10 big, steep steps
- At the top: pause, look around & enjoy the view
- Take the gentle cable-car back down
My daughter Filipa made a drawing for you:

So what’s the science behind all of this esoteric yoga quack, you might ask? Let me give you just a tiny bit of neurobiology background.
In humans, any response to fear is modulated by a brain structure called the amygdala. Very simply put, this is what the amygdala kicks off in a threatening situation:
- stress hormone levels increase
- breathing becomes shallow and rapid
- blood pressure and heart rate go up
- complex decision-making disappears
The amygdala (actually, it’s the amygdalae – we have two of them) are part of the limbic system. This is a group of brain structures which, evolutionarily, are rather old.
The important thing in the context of our breathing exercise is this: The amygdalae not only trigger a variety of responses, they also monitor bodily functions. As you probably know, we cannot willfully lower our stress hormone levels or influence our blood pressure. However, we can alter our breathing. If we manage to fully fill our lungs and slow our breathing – in stark contrast to the shallow and rapid breathing triggered by the amygdala – we signal the limbic system that everything is under control. It’s like telling the amygdala to “just chill”. It will trust the sensory input based on your lungs, and will in turn wind down all other stress responses, e.g. it will lower blood pressure and cortisol/adrenaline levels.
If you manage to mindfully observe your body’s reactions during and after the breathing exercise, you may even be able to notice how your whole body feels a lot calmer after just a few cycles.
Self-Compassion
How many times have you told yourself to calm down lately? That you shouldn’t be scared about COVID-19 because you live in a very safe country? That fear won’t get you anywhere? That you shouldn’t complain, because you have food on the table? That your worries are not helpful, and that you should keep quiet? That you should stop whining and just get on that yoga mat?
But: How do you treat a good friend or your children when they trust you with their sorrows?
You probably hear them out patiently. You give them your full attention, without judging their feelings. You acknowledge their suffering and give them a hug. You are just there for them, compassionately.
The thing is, you can do just that with yourself. With self-compassion, we give ourselves the same kindness and care we’d give to a good friend or our children.
Kristin Neff has many helpful exercises and a ton of excellent research around this topic. Most notably, having empathy for ourselves also creates more empathy for others. Empathy, love, and self-compassion are the last things we should ration right now!
Recommended reading: Self-Compassion: The Proven Power of Being Kind to Yourself by Kristin Neff
Recommended listening: Unlocking Us by Brené Brown
Cold Showers
At the end of your warm shower, turn the water very cold and stay underneath for 30 seconds.
Super simple, yet very good for your nervous system. Here’s why: The vagus nerve is one of the most important nerves in our body. It plays a powerful part in bringing our minds and bodies back to calm after encountering a perceived threat (in today’s time, new COVID-19 numbers can be very threatening).
Exposing your body to cold conditions, such as taking a cold shower, stimulates the vagus nerve. While your body adjusts to the cold, sympathetic activity (“fight-or-flight”) declines, while parasympathetic activity (“rest and digest”) increases.
Recommended reading: Nurturing Resilience by Kathy L. Kain and Stephen J. Terrell
Completing The Stress Cycle
While our ancestors were running from saber-toothed tigers, today’s stressors are very different: work problems, health concerns, money issues – the list goes on and on. We do our best to fix the problems and deal with the stressors, but our bodies stay stuck in the stress response.
The reason is that, evolutionarily, our bodies rely on the full circle of a stress response: Our ancestors ran from the tiger. After successful escape, they hugged their loved ones, shouted in triumph, or fell on the floor crying.
Our stressors have changed, but our body’s needs to deal with the stress are still the same: we need to complete the stress cycle. According to Emily & Amelia Nagoski, these are ways to do it:
- Physical activity
- Creativity
- Crying
- Laughing
- Physical affection
- Deep breathing
Recommended reading: Burnout by Emily & Amelia Nagoski
Turning Around Thoughts
As scientists, we stick to the facts. Our thinking is razor sharp, and we know what is true. Often, this is very important and helpful, and it is exactly what makes us good scientists. Simultaneously, our black & white thinking is very limiting. It turns us into narrow-minded, stubborn brats who can get lost in simplistic stories. Life is a complex beast, most problems can be tackled from different angles, and many things can be true at the same time.
The Work by Byron Katie is a very good practice to question your own thinking. It is a form of self inquiry which can be learned easily. While “The Work” involves several steps, the practice of turning around thoughts is the easiest part to get started. Let me give you a quick idea:
Based on your current believes, isolate your thoughts in a simple statement. For example, your thinking may go something like this:
«Rahel is a self-proclaimed scientist who should not spread bullshit like this.»
Now, turn your thoughts around. There are many possible turnarounds:
«Rahel is not a self-proclaimed scientist.»
«Rahel should spread bullshit like this.»
«Rahel should not spread knowledge like this.»
«I should not spread bullshit like this.»
«I myself am a self-proclaimed scientist.»
Ask yourself if any of these opposites is as true or truer than the original thought? Note that the purpose of this inquiry is not to prove you wrong – you have every reason and right to stick to your original thoughts. However, the turnarounds might each hold a tiny bit of truth and provide a new perspective. They may give you a little nudge to be more open-minded and make space for other opinions. Personally, this form of self inquiry often points me to some blind spots which I otherwise tend to avoid because of shame or fear.
Recommended reading: Loving What Is by Byron Katie
The Power Of Now
Our thinking, no matter how scientific, is never really in the now. We dwell in the past, or we make up stories for the future. Spinning up narratives is what our brain knows best. The mind feels like it is working in our best interest, but it is actually just inventing problems.
Here’s a great exercise I sometimes practice in bed, when I have trouble falling asleep. I got to know it through Sarah Wilson (who is actually quoting Eckhart Tolle):
«Ask yourself what ‘problem’ you have right now, not next year, tomorrow, or five minutes from now. What is wrong with this moment. Try this with a problem. Feel into the problem now, not in 60 seconds, not in 2 seconds. Now! Is the problem still there? Nope. It’s gone, right? Worries don’t exist in the now. Worries about the future or the past don’t exist either – they’re just narratives we create in the present.»
This exercise is a form of mindfulness meditation. There’s scientific evidence that it results in a gain of insulae connection strength. The insulae are brain structures believed to be involved in consciousness. They play a role in diverse functions, such as compassion & empathy, self-awareness, cognitive functioning, and interpersonal experience. The more activation in the insulae, the calmer we are.
Recommended reading: First, We Make the Beast Beautiful by Sarah Wilson
Professional Help
You made it this far, wow, thanks for reading. Please bear in mind that reading is the easy part. Scientists like you and me are very good at reading and rationalizing. But: These practices are called practices for a reason – they need practice. Just like we need to listen to epidemiologist when it comes to COVID-19, we should rely on professionals when it comes to mental health. Yoga teachers can guide you and provide more details on breathing techniques. Psychotherapists know a lot about the relationships between behavior, thoughts, and emotions. They can help you break cycles that cause suffering in everyday life. Please reach out for help if you are struggling.
Take care, y’all!
A CSS Subgrid Example
Whenever I hear about a new technology or language feature, the first question I ask myself is: Which problem does it solve? So when I learned about the addition of subgrid to the CSS Grid Layout specification, I wanted to see a simple example which showed a subgrid-based solution to an actual problem. I found helpful videos and rock-solid-but-complicated layout arrangements, but nothing simple.
This post is the 3’-intro I was looking for:
A Simple Form
Suppose you are dealing with the following HTML form:
<form>
<label for="name" class="field">
<span class="label-text">Name</span>
<input type="text" id="name" />
</label>
<label for="email" class="field">
<span class="label-text">Email</span>
<input type="email" id="email" />
</label>
<label for="message" class="field">
<span class="label-text">A Looong Label</span>
<input type="text" id="message" />
</label>
</form>The existing CSS Grid layout already makes it easy to arrange individual fields:
.field {
display: grid;
grid-template-columns: auto 1fr;
grid-column-gap: 1em;
margin-bottom: 1em;
}As a result, each row dynamically respects the preferred width of its label:

While this is a good start, we would like to have something better:
A two-column definition, so that
- the widest label determines the width of the left column
- all input fields are aligned in the right column

This is exactly what the new subgrid feature is for: It matches up its grid lines to lines in the parent grid. We move the two-column grid layout definition to the parent form, and tell the fields to align along these tracks:
form {
display: grid;
grid-template-columns: auto 1fr;
grid-column-gap: 1em;
}
.field {
display: grid;
grid-column: span 2;
grid-template-columns: subgrid;
margin-bottom: 1em;
}Caution: CSS Subgrid is only supported in Firefox (v71)
How we use React/Redux with TypeScript
Our team develops visual applications in the field of medical informatics. We started using React/Redux with TypeScript a few months ago. This post is a highly opinionated summary of best practices that evolved over time:
- Favor Types Over Classes
- Don’t Fear Stringly Types
- Favor Composition Over Inheritance
- Immutability FTW
- Nominal Typing
- Explicit Types Enhance Readability
- TSS: CSS + TypeScript = 😍
- Look Ma, No Semicolons!
A bit of personal background, to give certain decisions more context: I have been developing user interfaces for over 20 years. Java and OOP have been loyal companions throughout most of this time. A few years ago, I started doing more and more FP, mostly in Scala & Elm, but also in Java (hi vavr 👋).
Our team members come from all sorts of backgrounds. When deciding on a web app stack, opinions varied a lot. We finally settled on React/Redux + TypeScript as a compromise – it turned out to be a good decision.
Favor Types Over Classes
Coming from an OOP background, it was comforting that TypeScript brings familiar OOP constructs to the table. However, TypeScript is based on a structural type system, which can confuse Java developers very quickly:
class Patient {
firstName: string
lastName: string
constructor(firstName: string, lastName: string) {
this.firstName = firstName
this.lastName = lastName
}
}
const patient: Patient = { firstName: 'Ada', lastName: 'Lovelace' }
console.log(patient instanceof Patient) // false – seriously?! 🤔I am sure that one could get used to the TypeScript way of working with classes. However, we somehow ended up not using classes at all 🤷. Instead, we exclusively model our data with read-only types:
type Patient = Readonly<{
id: PatientId
caseId: CaseId
bed: BedId
firstName: string
lastName: string
}>Super concise and very safe to use.
Don’t Fear Stringly Types
Any experienced Java programmer avoids stringly types like the plague. In Java, this makes sense, they prevent the compiler from helping us find errors. The TypeScript compiler works differently, so be ready to embrace patterns which you would avoid in Java:
type Patient = Readonly<{
gender: 'male' | 'female' | 'non-binary'
}>Code completion works perfectly fine here:
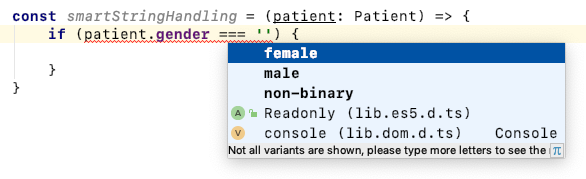
And the compiler detects errors flawlessly:
const smartStringHandling = (patient: Patient) => {
if (patient.gender === 'whatever') { // compile error
}
}To give a more advanced example, here’s how we base our action types, actions, and reducers on simple strings:
actionTypes.ts
const ADD_MESSAGE = 'message/add'
const ADD_TODO = 'todo/add'actions.ts
type Action = AddMessageAction | AddTodoAction
type AddMessageAction = Readonly<{
type: typeof ADD_MESSAGE
message: Message
}>
type AddTodoAction = Readonly<{
type: typeof ADD_TODO
todo: Todo
}>reducer.ts
const reducer = (state: State, action: Action): State => {
switch (action.type) {
case ADD_MESSAGE:
// 🎉 this would require a cast in Java
const message = action.message
return {
...state,
messages: state.messages.push(message)
}
case ADD_TODO:
return {
...state,
todos: state.todos.push(action.todo)
}
}
}Favor Composition Over Inheritance
As mentioned above, we don’t really use TypeScript’s OOP features, so using inheritance has never been very tempting. Instead, we often use a mix of composition, union types, and intersection types to foster code re-use:
type Patient = Readonly<{
address: Address // Composition
gender: 'male' | 'female' | 'non-binary' // Union Type
}>
type Displayable = Readonly<{
displayName: string
}>
type DisplayablePatient = Patient & Displayable // Intersection TypeImmutability FTW
We haven’t seen many runtime errors, but the ones that occurred were all caused by inconsistent mutations. That’s why we settled on using the immutable collections library to make all our state completely read-only:
import { Map } from 'immutable'
type State = Readonly<{
bedByPatient: Map<PatientId, BedId>
}>Nominal Typing
Using type aliases for your identifiers seems very convenient. No need for extra wrapping, and very readable code:
type PatientId = string
type BedId = string
type State = Readonly<{
bedByPatient: Map<PatientId, BedId>
}>Unfortunately, things look more type-safe than they are. Aliases are nothing more than what their name implies: they are simple synonyms. Any string can be used in place of a PatientId or BedId – and vice versa:
const state: State = {
bedByPatient: Map<PatientId, BedId>()
}
// Compiles just fine, which is NOT what we want
state.bedByPatient.set('foo', 'bar')We want to have types which can be distinguished by the compiler because they have different names, even though they share the same structure (a string). This is known as “nominal typing”. The TypeScript Deep Dive Book gives a good list of nominal typing patterns.
We are using the enum-based brand pattern to get the desired compile-time safety:
enum PatientIdBrand {}
type PatientId = PatientIdBrand & string
enum BedIdBrand {}
type BedId = BedIdBrand & string
type State = Readonly<{
bedByPatient: Map<PatientId, BedId>
}>
const state: State = {
bedByPatient: Map()
}
// Compile error:
// Argument type '"foo"' is not assignable to parameter of type 'PatientId'
state.bedByPatient.set('foo', 'bar')Explicit Types Enhance Readability
While it is often possible to not specify types explicitly, they still sometimes enhance code readability (and IDE completion, for that matter). Container components are a good example: they involve a lot of “plumbing”, where input/output types have to match, so explicit types are a plus here. This is how our container components tend to look:
type Props = Readonly<{
patientId: PatientId
}>
type FromStateProps = Readonly<{
patient: Patient
}>
const mapStateToProps = (state: State, props: Props): FromStateProps => {
const patient = getPatient(state, props.patientId)
return {
patient
}
}
type FromDispatchProps = Readonly<{
onMouseEnter: () => void
onMouseOut: () => void
}>
const mapDispatchToProps = (dispatch: Dispatch<PatientsAction>, props: Props): FromDispatchProps => {
return {
onMouseEnter: () => dispatch(selectPatients(ImmutableList.of(props.patientId))),
onMouseOut: () => dispatch(selectPatients(ImmutableList()))
}
}
export default connect(mapStateToProps, mapDispatchToProps)(ExampleComponent)TSS: CSS + TypeScript = 😍
As a developer, CSS has always been the scary corner of my applications. It uses a global namespace, you cannot use variables, and it’s almost impossible to tell which code is even in use at all. So you end up treating your CSS very differently from the rest of your code: no refactorings, no re-use, no clean-up.
We are using Material-UI in all our projects, so it did not take much convincing to also use their styling solution. It uses JSS at its core and has excellent TypeScript support. This is how a basic component looks:
import { createStyles, withStyles, WithStyles } from '@material-ui/core'
import * as React from 'react'
const styles = createStyles({
root: {
backgroundColor: 'steelblue'
}
})
type Props = Readonly<{
text: string
}> & WithStyles<typeof styles>
const ExampleComponent = ({ text, classes }: Props) =>
<div className={classes.root}>{text}</div>
export default withStyles(styles)(ExampleComponent)Look Ma, No Semicolons!
And finally, a good practice that is not specific to React nor TypeScript: make your code prettier! We use husky to kick off code formatting before each git commit. Here’s our current configuration:
.prettierrc:
Thanks for reviewing this post, Ben!
Older Posts » Archive