JavaFX 3D Line

I have no experience in 3D programming whatsoever. Last week, I took my first steps in JavaFX 3D, but hit a wall when I wanted to draw a line between two points: There is no Line shape! The only out-of-the-box Shape3D classes are Box, Cylinder, Sphere, and MeshView – wow…

Well, it shouldn’t be too difficult to connect the points with a slender cylinder, right?

I was wrong, it took me an embarrassingly long time to get the trigonometry right :-)

Here’s my magic crutch:

public Cylinder createConnection(Point3D origin, Point3D target) {
    Point3D yAxis = new Point3D(0, 1, 0);
    Point3D diff = target.subtract(origin);
    double height = diff.magnitude();

    Point3D mid = target.midpoint(origin);
    Translate moveToMidpoint = new Translate(mid.getX(), mid.getY(), mid.getZ());

    Point3D axisOfRotation = diff.crossProduct(yAxis);
    double angle = Math.acos(diff.normalize().dotProduct(yAxis));
    Rotate rotateAroundCenter = new Rotate(-Math.toDegrees(angle), axisOfRotation);

    Cylinder line = new Cylinder(1, height);

    line.getTransforms().addAll(moveToMidpoint, rotateAroundCenter);

    return line;
}

To illustrate what’s going on, I created a 2D representation of all individual steps, starting off with the creation of the cylinder. By default, its center is placed at the origin:

The moveToMidpoint transformation moves its center to the final location (the yellow midpoint in the above image):

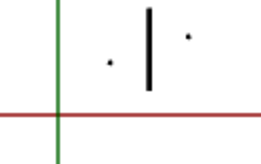
And finally, the rotateAroundCenter transformation corrects the cylinder’s direction:

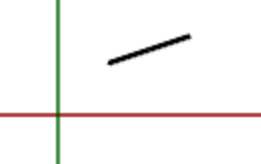
Obviously, the tricky part is finding the proper axis and angle of rotation. Both are calculated relative to the yAxis because of the cylinder’s initial direction. The axisOfRotation must be perpendicular to the plane defined by the yAxis and the diff vector. To find such a perpendicular vector, we can (by definition) calculate the cross product of the two vectors. In the 2D case, the result is equivalent to the z-axis, but in 3D it may be tilted.

The angle is calculated based on the dot product (aka scalar product) of the two vectors, which is defined by

A • B = |A| |B| cos(alpha)

If A and B are both unit vectors, this becomes

A • B = cos(alpha)

which we can resolve to

alpha = acos(A • B)

That’s it!